

The second term is then the rate at which probability is flowing out of the volume V. This equation holds for charges of either sign, because we define the area vector of a closed.
Derive electric flux formula free#
In particular, if Ψ is a wavefunction describing a single particle, the integral in the first term of the preceding equation, sans time derivative, is the probability of obtaining a value within V when the position of the particle is measured. According to Gauss’s law, the flux of the electric field E through any closed surface, also called a Gaussian surface, is equal to the net charge enclosed ( q enc) divided by the permittivity of free space ( 0): Closed Surface q enc 0. This is the conservation law for probability in quantum mechanics. Where V is any volume and S is the boundary of V. J = j e / q = 1 2 m + μ S q s ℏ ∇ × ( Ψ ∗ S Ψ ) In non-relativistic quantum mechanics, the probability current j of the wave function Ψ of a particle of mass m in one dimension is defined as Definition (non-relativistic 3-current) Free spin-0 particle The concept of probability current is also used outside of quantum mechanics, when dealing with probability density functions that change over time, for instance in Brownian motion and the Fokker–Planck equation. Thus, the dimensional formula of electric flux is M1 元 T-3 I-1. The probability current is invariant under gauge transformation. the probability current density) is related to the probability density function via a continuity equation. The electric flux density, D, is then equal to the electric flux emanating from the charge, q, divided by the area of the sphere. Gauss’s law for electricity states that the electric flux across any closed surface is proportional to the net electric charge q enclosed by the surface that is, q/0, where 0 is the electric permittivity of free space and has a value of 8.854 × 1012 square coulombs per newton per square metre. As in those fields, the probability current (i.e. Gauss’s law, either of two statements describing electric and magnetic fluxes. Probability currents are analogous to mass currents in hydrodynamics and electric currents in electromagnetism. It is a real vector that changes with space and time. Details of the calculation: The charge distribution is spherically symmetric and so the electric field is E(r) E(r) r/r. Specifically, if one thinks of probability as a heterogeneous fluid, then the probability current is the rate of flow of this fluid.
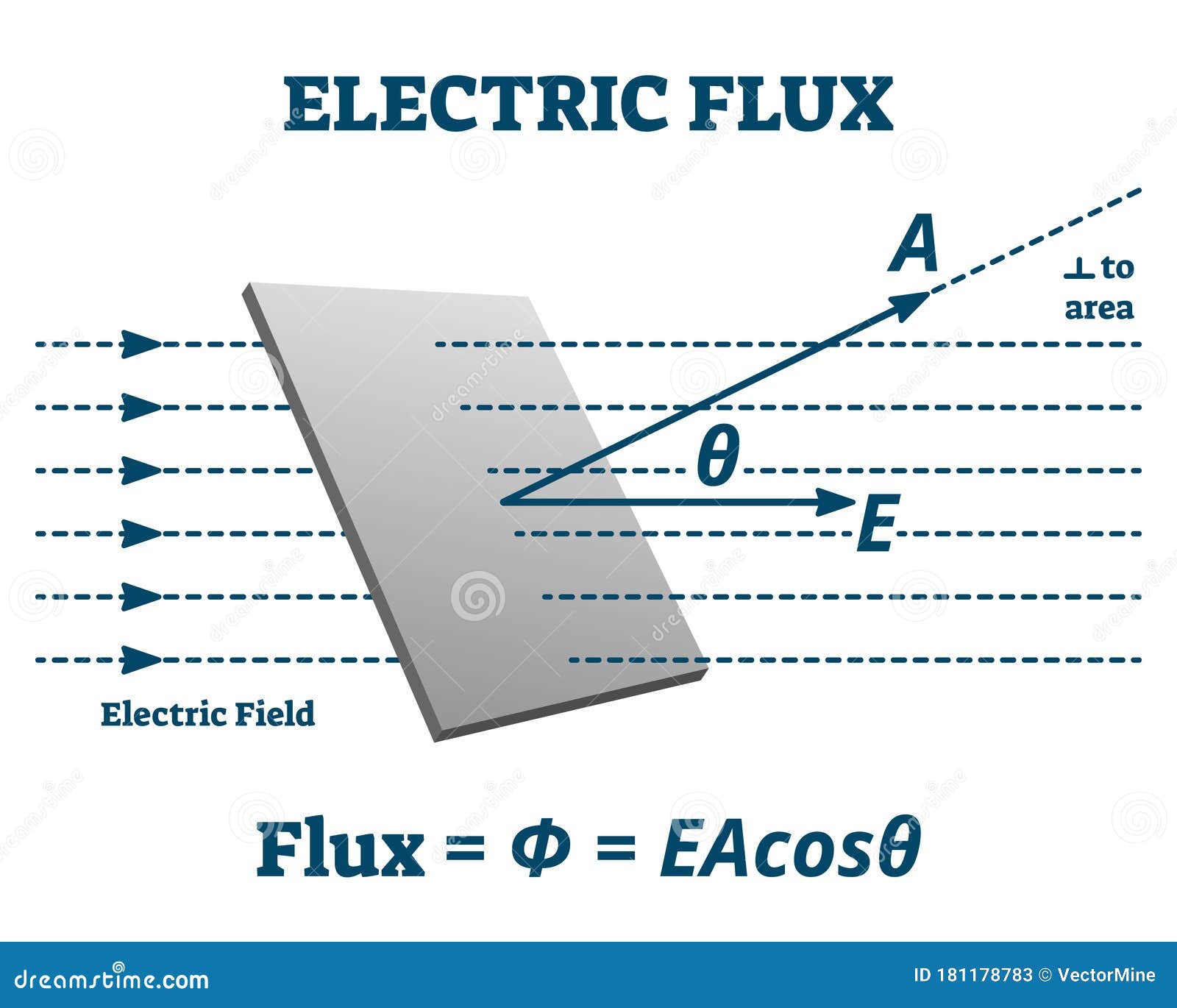
Both of them formulated this law in the context of the attraction of ellipsoids. This law was formulated by Joseph Lagrange in 1773, followed by Carl Gauss in 1813. It is used to relate the distribution of charge with the resulting electric field due to the charge.

In quantum mechanics, the probability current (sometimes called probability flux) is a mathematical quantity describing the flow of probability. Gauss law is a very important part of electromagnetism and physics.


 0 kommentar(er)
0 kommentar(er)
